Bart H. McGuyer
Deriving the LTR primary capacitance formula for NSTs
TLDR: Derivation of a common formula used with Tesla coils.
While working on a project that used a neon sign transformer (NST) to repetitively charge and discharge a bank of capacitors, I needed to determine the maximum capacitance \(C_\text{max}\) the bank could have without reducing the charging voltage. Approximating the NST as an ideal power supply (it isn't ...) led to a really simple formula for \(C_\text{max}\). After doing this, I remembered that there is a formula for a capacitance \(C_\text{LTR}\) commonly used to design Tesla coils that should apply, even though that wasn't what I was building. Surprisingly, the two formulas are nearly identical. I realized I didn't know where the Tesla coil formula came from, so I thought I'd dig in more. Here's what I found.
First, let's derive \(C_\text{max}\). Consider an AC power supply with frequency \(f\) (e.g., 60 Hz), rated output power \(P = V_\text{rms} I_\text{rms}\) and output impedance \(Z = V_\text{rms}/I_\text{rms}\), where \(V_\text{rms}\) and \(I_\text{rms}\) are the maximum root-mean-square output voltage and current used to specify NSTs. Then \(C_\text{max}\) corresponds to the capacitance that charges from zero voltage up to \(\sqrt{2}\, V_\text{rms}\) during a quarter cycle, or \(1/(4f)\) seconds, at the power \(P\). Energy conservation requires \((1/2) C_\text{max} (\sqrt{2} \, V_\text{rms})^2 = P / (240~\text{Hz}),\) giving $$C_\text{max} = 1/(4 f Z).$$ For 60 Hz AC, \(C_\text{max} = 1/(Z \times 240~\text{Hz}).\) This result assumes the supply is a sine-wave voltage source (see Figure 1) and that its current does what's needed so the time-averaged power over a quarter cycle is \(P\).
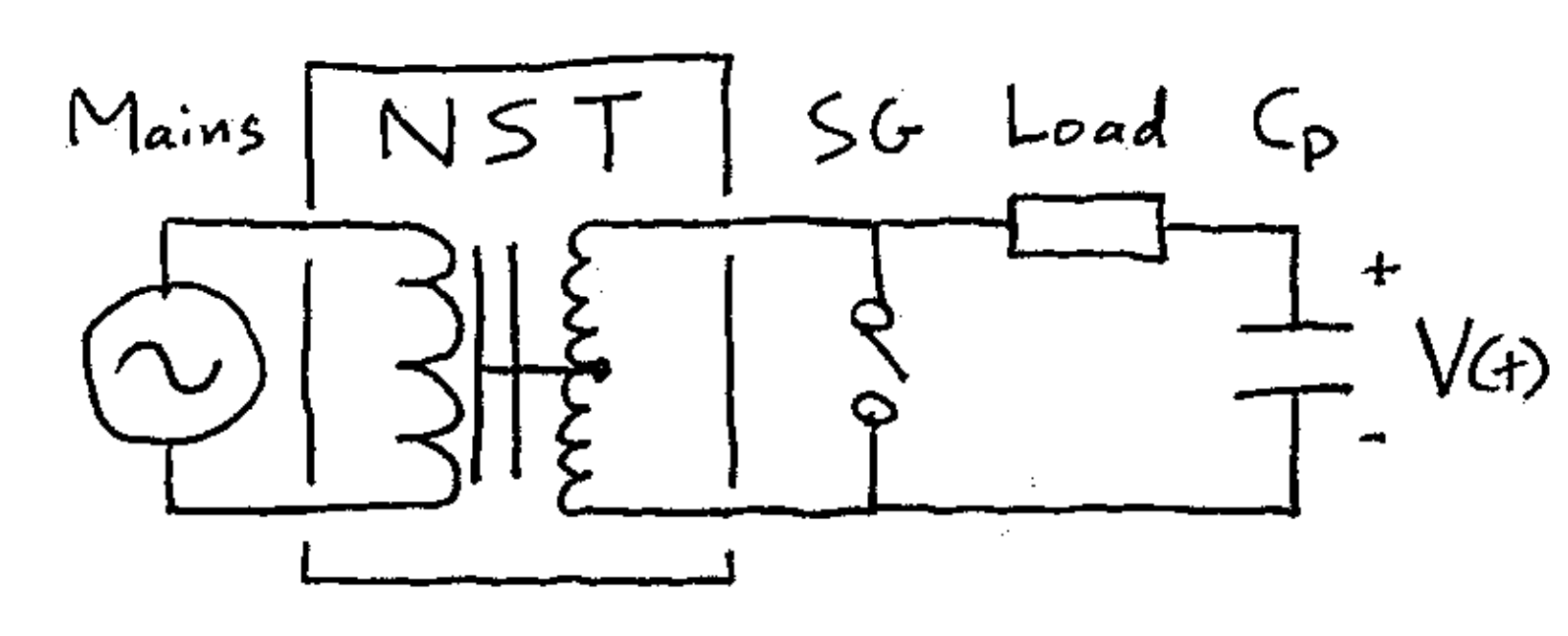
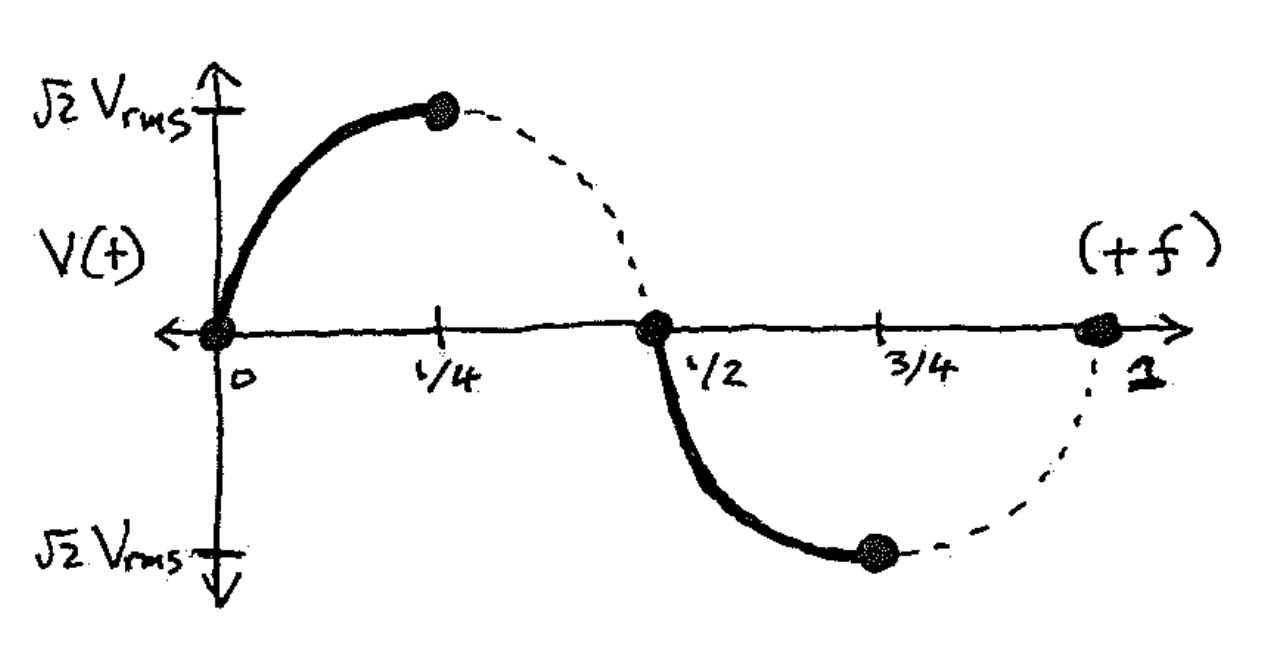
Figure 1: (Left) Example circuit for NST charging of the primary capacitor \(C_p\) in a Tesla coil. Acronyms: NST: neon sign transformer; SG: spark gap. (Right) Solid curves are the voltage across \(C_p\) during charging, assuming the NST acts as an ideal sine-wave voltage source and the "Load" is negligible. In a Tesla coil, this voltage would not follow the dashed curves because of the spark gap firing.
Next, here's background on the Tesla coil formula. While designing a spark-gap Tesla coil, one step is to choose the primary tank circuit's capacitance \(C_p\), which controls the amount of energy in each operational cycle (the "bang size"). For simple static spark gaps often used with NSTs, the recommended choice for \(C_p\) is $$C_\text{LTR} = 1.6 / (2 \pi f Z),$$ which is called the static-gap "larger-than-resonant" (LTR) capacitance [1]. The rounded factor of "1.6" seems to be the original choice, but sometimes is replaced with another value between 1.5 and 2.0. For 60 Hz AC, \(C_\text{LTR} \approx 1 / (Z \times 236~\text{Hz})\) which is almost identical to \(C_\text{max}\) above.
The similarity between \(C_\text{LTR}\) and \(C_\text{max}\) is not accidental. It took some digging, but you can read about the origins of \(C_\text{LTR}\) in [2-3]. In short, \(C_\text{LTR}\) first came from computer simulations of NST charging in Tesla coils [4]. These simulations seem to have treated the NST as a simple transformer (with nearly unity coupling) that behaves like an ideal power supply until the spark gap fires. \(C_\text{LTR}\) then came from finding the capacitances that gave 120 breaks per second (BPS) for each NST (i.e., charging in a quarter cycle). Moreover, a little later, \(C_\text{LTR}\) was justified analytically with essentially the same derivation as that given for \(C_\text{max}\) above [3]. So, the two formulas should be identical — neat!
Since it's so hard to find the derivation of \(C_\text{LTR}\) [3], and it doesn't seem to be well known, I thought it'd be worth sharing this note. Last but not least, before you use these formulas, remember that NSTs are not ideal power supplies, so the optimal primary capacitance \(C_p\) will come from trial and error (thus the varying factor of "1.6") [5]. \(C_\text{LTR}\) and \(C_\text{max}\) are just design guides to help get you started.
References- [1] Tesla coil design programs like Javatc usually calculate \(C_{LTR}\).
- [2] 4HV post in thread, "Calculating LTR", by Terry Fritz, 9/10/2006.
- [3] TCML post, "Theoretically, Cltr/Cres = pi/2", by Terry Fritz, 4/1/2002.
- [4] Webpage, "This is a computer study of NST charging circuits", by Terry Fritz, 9/9/2000 (archived by capturedlightning.org).
- [5] PDF, "Experiment to determine best capacitor size in a Tesla coil when using a static gap", by Gary Lau, 10/23/2010.
(January 2018; updated April 2018)
© , bartmcguyer.com